邮箱:caohy19@lzu.edu.cn
编者按:本文主要摘译自下文,特此致谢!
Source:Lokshin M, Sajaia Z. Maximum likelihood estimation of endogenous switching regression models[J]. The Stata Journal, 2004, 4(3): 282-289. -PDF-
目录
3. 论文中的应用
4. 相关命令介绍
5. Stata 范例
6. 参考文献
温馨提示: 文中链接在微信中无法生效。请点击底部「阅读原文」。或直接长按/扫描如下二维码,直达原文:
1. 简介
在多数实证研究中,个体观测很可能是一个选择后的结果,例如是否加入工会、是否在公共部门就业或是否买房。由于只能观测到个体的选择行为以及选择后的结果,直接将结果变量对决策变量回归可能存在遗漏变量的内生性问题。为了缓解上述问题对实证研究的影响,本文将介绍一种通过设定转换方程对决策变量建模的方法,即内生转换模型。
2. 内生转换模型2.1 模型设定与 ML 估计
在内生转换模型中,需要构建两个回归模型,以及一个示性函数。其中,个体决策结果由示性函数决定。具体如下:
其中,
0 \I = 0 quad text{if} gamma_{i}Z_{i}+u_{i} leq 0end{aligned}” data-formula-type=”block-equation”>
是连续的被解释变量, 和 是外生变量向量,、 和 是待估计的参数。三个方程中的干扰项 、 和 满足零均值的联合正态分布,并且相关系数矩阵为:
其中, 为选择方程中干扰项的方差, 为连续方程中干扰项方差, 为选择方程和连续方程干扰项的协方差。由于两种 无法同时观测,因此没有定义二者干扰项之间的协方差。在给定方差的分布后,模型的对数似然函数为:
其中,
是某种权重, 是选择方程干扰项和连续方程干扰项的相关系数。为了将 的估计限定在 -1 到 1 之间, 始终为正,并且 ML 直接估计的是 ,以及 。
2.2 预测
除了参数估计外,内生转换模型还有一项重要的工作是预测不同状态下结果变量的情况。其中,无条件期望的预测为:
条件期望的预测为:
条件期望在部分情况下是对可观测结果的预测,但也包含了对不可观测情形下选择结果的预测。
3. 论文中的应用3.1 差距估算
万相昱等 (2021) 对公共部门和私人部门的工资差距进行了估计。其内生转换模型为:
在估计了内生转换模型后,万相昱等 (2021) 又对部门工资的无条件期望进行了预测,进而得到公共部门和私人部门的拟合工资:
最后,近似计算了部门之间的工资差异。由于被解释变量是对数值,首先需要进行反对数计算:
3.2 估计处理效应
李亚娟和马骥 (2021) 使用内生转换模型,来估计采纳科学施肥技术处理组和控制组的平均处理效应。具体来看,分别用 和 表示是否采纳科学施肥技术和不同选择下的收入,内生转换模型表示为:
根据估计结果,进一步应用内生转换模型预测了不同条件下的被解释变量。在可观测条件下,预测式是:
不可观测条件下,预测反事实:
从而可以定义处理组和控制组的平均因果效应:
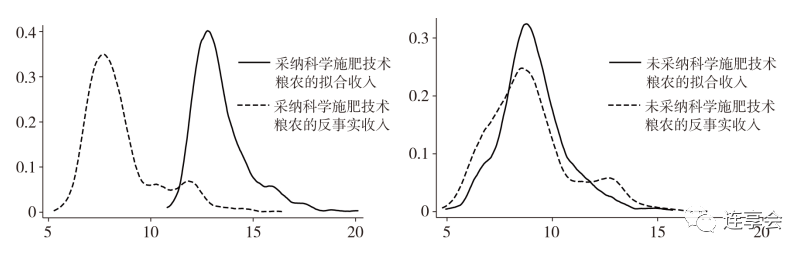
文中还绘制了不同条件下的收入分布情况,可以直观表现采纳科学施肥技术对收入分布的影响效果,效果如下图。
4. 相关命令介绍
*命令安装
ssc install movestay, replace
*命令语法
movestay (depvar1 [=] varlist1) [(depvar2 [=] varlist2)] [weight] [if
exp] [in range] , select(depvar_s [=] [varlist_s]) [robust
cluster(varname) maximize_options]
其中,
上述命令设定连续方程形式和选择方程形式,当连续方程中加入的变量相同时,只需要设定一次。
内生转换模型估计结束后,可以使用 mspredict 进行预测。
*命令安装
net install st0071_2, replace
*命令语法
mspredict newvarname [if exp] [in range], statistic
5. Stata 范例
本例对应的研究是,在公共部门和私人部门就业对工资的影响。由于工资是就业部门选定后的结果,因此存在内生性问题。该模型的设定为:
其中, 是个体选择的潜变量, 是在不同部门的工资对数值, 是决定部门选择的因素, 是影响部门工资的因素。可以观测的选择结果与潜变量之间的关系为:
0 \I_{i} &= 0 quad if otherwiseend{aligned}” data-formula-type=”block-equation”>
直接估计该模型的问题是,可能存在不可观测的因素同时影响部门选择和个体工资,忽略这些选择效应很容易得出错误的结论。
本文使用的数据集中共包含了 12 个变量。其中,private 表示就业选择,如果个体在私有部门就业则取 1,否则取 0;被解释变量 lmo_wage 是月工资的对数值。估计连续方程使用的外生变量主要来自 Minser 方程,纳入年龄及其平方项 age-age2,教育水平虚拟变量 edu4、edu5 和 edu13,地区变量 reg2-reg4。估计选择方程使用的数据是婚姻情况 m_s1 和家庭成员就业情况 job_hold。
首先使用 ML 估计内生转换模型:
. lxhuse movestay_example.dta ,clear
. movestay lmo_wage age age2 edu13 edu4 edu5 reg2 reg3 reg4, ///
> select(private = m_s1 job_hold) // 估计内生转换模型
Endogenous switching regression model Number of obs = 2094
Wald chi2(8) = 102.43
Log likelihood = -2470.9304 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
lmo_wage_1 |
age | 0.042 0.029 1.45 0.147 -0.015 0.100
age2 | -0.001 0.000 -1.55 0.121 -0.001 0.000
edu13 | 0.344 0.279 1.23 0.219 -0.204 0.891
edu4 | -0.158 0.161 -0.98 0.326 -0.473 0.157
edu5 | -0.164 0.130 -1.26 0.207 -0.419 0.091
reg2 | -0.286 0.110 -2.61 0.009 -0.502 -0.071
reg3 | 0.708 0.143 4.96 0.000 0.428 0.987
reg4 | -0.138 0.141 -0.98 0.328 -0.416 0.139
_cons | 7.416 0.481 15.42 0.000 6.473 8.358
-------------+----------------------------------------------------------------
lmo_wage_0 |
age | -0.037 0.011 -3.32 0.001 -0.059 -0.015
age2 | 0.000 0.000 2.91 0.004 0.000 0.001
edu13 | -0.507 0.089 -5.72 0.000 -0.680 -0.333
edu4 | -0.411 0.051 -8.08 0.000 -0.510 -0.311
edu5 | -0.297 0.039 -7.59 0.000 -0.374 -0.221
reg2 | -0.378 0.042 -8.99 0.000 -0.460 -0.296
reg3 | 0.705 0.053 13.26 0.000 0.601 0.810
reg4 | -0.236 0.047 -4.96 0.000 -0.329 -0.143
_cons | 9.322 0.238 39.21 0.000 8.856 9.788
-------------+----------------------------------------------------------------
private |
age | -0.146 0.026 -5.62 0.000 -0.196 -0.095
age2 | 0.001 0.000 4.47 0.000 0.001 0.002
edu13 | 0.076 0.246 0.31 0.757 -0.406 0.558
edu4 | 0.069 0.142 0.49 0.626 -0.208 0.346
edu5 | 0.235 0.106 2.21 0.027 0.027 0.444
reg2 | -0.440 0.096 -4.59 0.000 -0.628 -0.252
reg3 | -0.596 0.119 -5.02 0.000 -0.829 -0.363
reg4 | -0.601 0.113 -5.33 0.000 -0.822 -0.380
m_s1 | 0.157 0.092 1.70 0.088 -0.024 0.338
job_hold | 0.055 0.036 1.53 0.127 -0.016 0.126
_cons | 2.505 0.579 4.33 0.000 1.371 3.640
-------------+----------------------------------------------------------------
/lns1 | -.5903432 .0562427 -10.50 0.000 -.7005769 -.4801095
/lns2 | -.4220208 .0186565 -22.62 0.000 -.4585869 -.3854546
/r1 | .1456952 .3195504 0.46 0.648 -.480612 .7720024
/r2 | 1.353759 .0813975 16.63 0.000 1.194222 1.513295
-------------+----------------------------------------------------------------
sigma_1 | .5541371 .0311662 .4962989 .6187156
sigma_2 | .6557204 .0122335 .6321763 .6801414
rho_1 | .144673 .3128621 -.4467336 .6480923
rho_2 | .8749375 .0190864 .8318838 .907522
------------------------------------------------------------------------------
LR test of indep. eqns. : chi2(1) = 86.94 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
可以看出,Stata 同时汇报了两个连续方程和选择方程的估计结果。我们可以根据系数的显著性解读模型结果,进而确定哪些因素影响了私人、公共部分的工资以及个体关于就业部门的选择。不过,更为重要的是通过预测来估算部门间的工资差距和处理效应。
首先进行无条件预测,并估计部门之间的工资差异。根据计算结果可知,私人部门的工资比公共部门高 0.012 个水平值。
. mspredict lnwage1, xb1 // 私人部门的对数工资
. mspredict lnwage0, xb2 // 公共部门的对数工资
. tempvar w_np w_p
. gen `w_p' = exp(lnwage1) // 私人部门工资反对数值
. gen `w_np' = exp(lnwage0) // 公共部门工资反对数值
. gen w_diff = (`w_np'-`w_p')/`w_p' // 个体工资差异
. qui sum w_diff // 求平均工资差异
. dis "私人部门与公共部门的工资差异为:`r(mean)' "
私人部门与公共部门的工资差异为:.0117846367684842
接下来进行条件预测潜在结果,并估计 ATT 和 ATUT。可以看出,二者的估计结果分别为 -0.765 和 0.133,即进入私人部门的个体如果在公共部门工作,平均收入可能上升。
. mspredict yc11, yc1_1 // 私人部门工作的个体在私人部门就业收入的预测
. mspredict yc10, yc1_2 // 公共部门工作的个体在私人部门就业收入的预测
. mspredict yc01, yc2_1 // 私人部门工作的个体在公共部门就业收入的预测
. mspredict yc00, yc2_2 // 公共部门工作的个体在公共部门就业收入的预测
. qui sum yc11
. local yc11_m = r(mean)
. qui sum yc01
. local yc01_m = r(mean)
. dis "ATT = mean(yc11) - mean yc(01) = " `yc11_m'-`yc01_m'
ATT = mean(yc11) - mean yc(01) = -.76548519
. qui sum yc10
. local yc10_m = r(mean)
. qui sum yc00
. local yc00_m = r(mean)
. dis "ATT = mean(yc10) - mean yc(00) = " `yc10_m'-`yc00_m'
ATT = mean(yc10) - mean yc(00) = .13282834
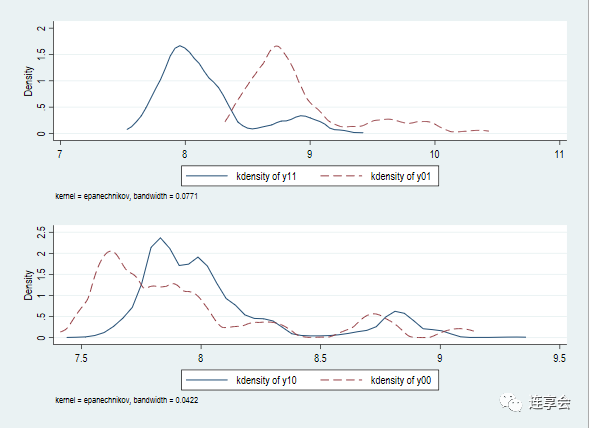
最后可以应用如下代码绘制不同分组的收入密度函数图像,来进行直接比较。
kdensity yc11,legend(label(1 "kdensity of y11") label(2 "kdensity of y01") col(2)) ///
title("") xtitle("") addplot(kdensity yc01,lp(dash)) saving(graph1.gph,replace)
kdensity yc10,legend(label(1 "kdensity of y10") label(2 "kdensity of y00") col(2)) ///
title("") xtitle("") addplot(kdensity yc00,lp(dash)) saving(graph2.gph,replace)
graph combine graph1.gph graph2.gph ,cols(1)
6. 参考文献
扫码加入连享会微信群,提问交流更方便
限时特惠:本站每日持续更新海量各大内部网赚创业教程,会员可以下载全站资源点击查看详情
站长微信:11082411

